To lead us into this, I will open with an analogy for those who aren't maths savvy (like me) and who prefer to see comparisons to explain concepts (also like me.).
Think of the bow's limb as the path ridden by a cyclist on a pushbike.
Think of the speed of the cyclist as the thickness of a bow's limb.
Think of the curve the bike can turn as the bend of the bow's limb
Think of any skidding or sliding the bike does as set or breakage if the cyclist falls.
Think of the angle that the cyclist needs to lean over when turning as the amount of stress in the bow's limb.
Now we've got that out of the way, I can explainerise:
A cyclist travelling in a straight line can go as fast as they want (a straight beam can be as thick as it wants)
When the cyclist goes around a corner (the limb bends) the cyclist must lean over into the curve (the limb experiences stress.)
If the cyclist is going very fast (very thick limb) there is a limit of curve that the can turn (a limit to the bend). Usually, this curve is quite large, even if the cyclist leans over a lot.
If the cyclist is travelling slowly (thin limb), the cyclist can travel a much tighter curve for the same amount of lean, or travel the same curve and lean a lot less.
A cyclist who is travelling just above stall speed can almost ride around themselves in circles without much leaning at all. (think of wood shavings)
Picture a particular cyclist travelling at a particular (high) speed and leaning over a certain amount. As the cyclist slows down, the curve which they travel will get tighter and tighter until the bike stops.
If this could be mapped, or seen from above, the path of the bike would likely look like an elliptically tillered bow limb.
If the cyclist was to travel at a constant speed (same thickness) and wanted to lean a consistent degree (equal stress) his path (tiller shape) would be circular.
Hopefully that is clear enough for most of you. I can clarify if need be.
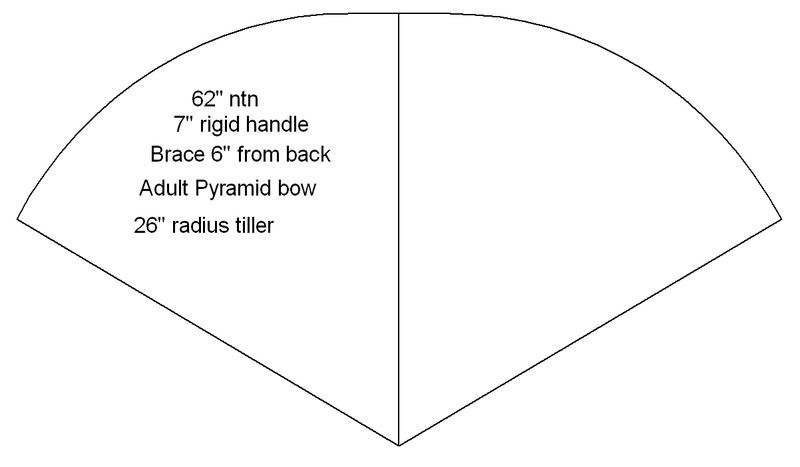
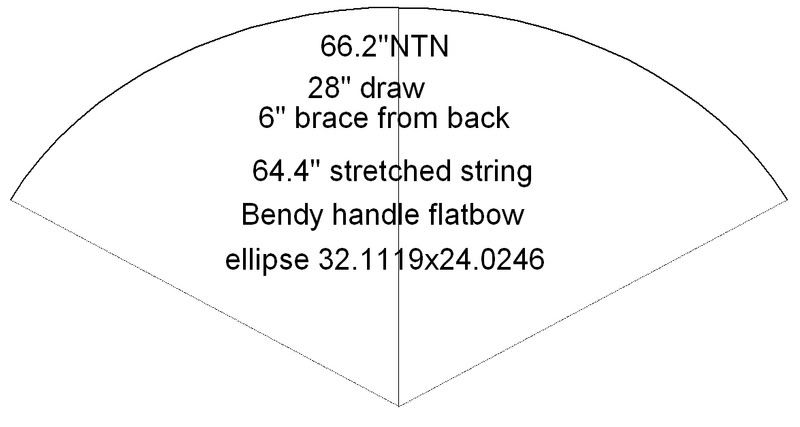
Now onto the mathsy part. For this example I will use a 66" bendy handle longbow and a 62" rigid handle pyramid bow. This assumes that the cross section of both bows is rectangular.
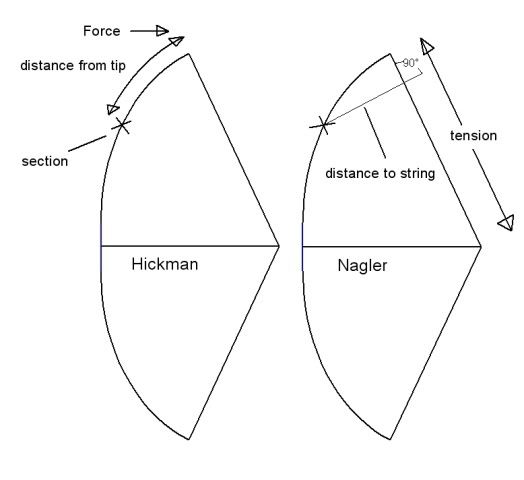
For any given piece of wood, the maximum amount of bend it can take is related to its thickness, the stress and the stiffness. The formula for this is
R/T=E/2S
Where
R=radius of curvature
T=thickness
E=modulus of elasticity
S=stress
As a beam is bent, it is subjected to progressively more and more stress (duh). It is most advantageous for a bow's limb to bending just to the point where set starts to appear. This is known as the elsatic limit. Lower than this and the bow is overbuilt, more than this and the bow experiences cast-robbing set.
As the stiffness of a beam is constant regardless of dimension, as is the desired stress, the formula can be written
C=R/T, where C is a constant found by dividing the stiffness by twice the allowable stress.
Thus, if the design of a bow is prepared, where the radii of curvature are known for many points along the limb, the maximum thickness allowable for that radius can easily be calculated.
NOTE: no rigid handle is ever truly 'rigid'. All wood bow handles bend somewhat, but not always noticeably. Thus, a 'stiff' handle will still have a radius of curvature, though it will be very large. Given below is a table showing the radius of curvature along a pyramid bow, and a bendy handle longbow.
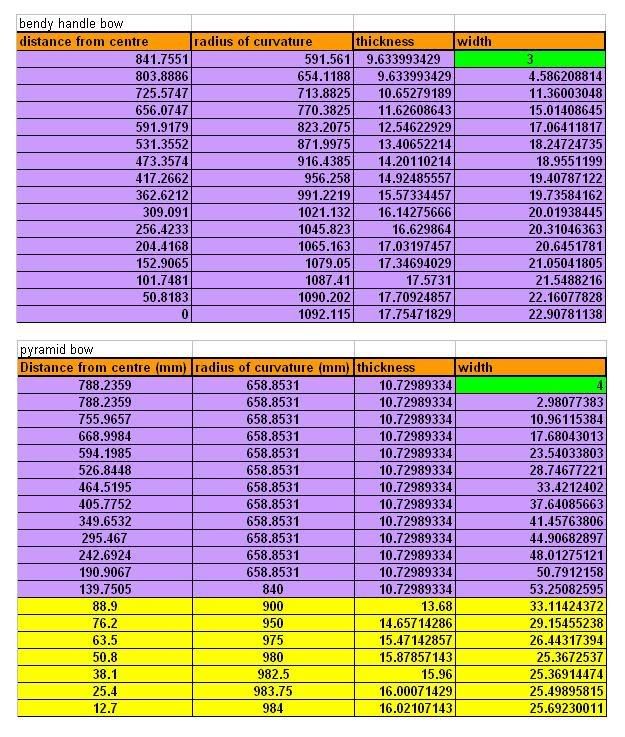
For the handle of a pyramid bow to be stiff, it must increase in thickness, i.e. the radius must increase. This cannot be an abrupt change, as wood will break at the junction. Rather, a smooth transition is required. If this ratio of thickness, radius and C is maintained throughout the handle and is not added to, i.e. made thicker, then the entire bow will experience even stress. Notice how for the limb, the radius of curvature is the same, due to the circular tiller. This means that the thickness will remain the same throughout the limb. Most bowyers, however, will overbuild a handle, meaning it will experience less stress than other parts of the limb. That's fine, there's nothing wrong with that, but this 'article' is supposed to be showing how equal stress is achieved
To find the width of the limb, a fancy schmancy formula is used using all the values thus discussed, and more. It involves knowing the distance from the string in a perpendicular line to the bow limb, the tension in the string, desired draw weight and so on. Of interesting note is that if the bow is required to be twice the draw weight, the whole bow will be twice as wide, including the handle.
The tables above also show the resulting widths for the limbs got from the formulas. Both bows have the same draw length and weight, and are made from the same theoretical piece of wood, which is actually close to a real test sample I did. The bendy handle bow, owing to its increased radius of curvature toward the grip, does not need to be widened as much as the pyramid bow to experience the same stress. Notice how at the very middle of both bows the dimensions are nearly the same, but the bendy handle bow is much narrower in the inner half of the limb. Looking at the two tiller shapes, I'd say that the pyramid, rigid handle bow was the 'C' shape, and the bendy handle bow the 'D' shape.
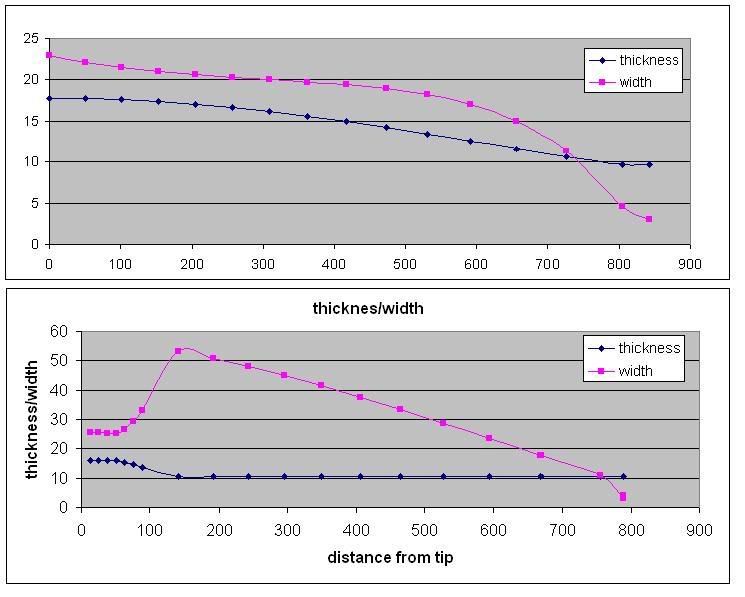
That's a pretty rushed explanation; I hope it's clear to at least some of you out there. If it's like mud to everyone, I'll try again be taking more time to explainify myself.
Cheers,
Dave
PS: actual wood smaple can vary greatly in their mechanical properties to those published in the books. Other smaples may be exactly the same.
The MoE is quite simple to calculate. So too is the MoR, which uses most of the same data as the stiffness test. If you (whoever has read this far)
want, I will write about how to calculate the MoR and elastic limit of a sample of wood, using two different methods.